Draw a Circle Without Floating Point Arithmetic in C

Rasterizing a circle of radius 23 with the Bresenham midpoint circumvolve algorithm. Only the dark-green octant is actually calculated, information technology'southward simply mirrored eight times to form the other seven octants.

A circle of radius 23 drawn by the Bresenham algorithm

In computer graphics, the midpoint circumvolve algorithm is an algorithm used to determine the points needed for rasterizing a circle. Bresenham's circumvolve algorithm is derived from the midpoint circle algorithm.^{[ citation needed ]} The algorithm tin be generalized to conic sections.^[ane]

The algorithm is related to work past Pitteway^[2] and Van Aken.^[3]

Summary [edit]

This algorithm draws all eight octants simultaneously, starting from each key management (0°, 90°, 180°, 270°) and extends both ways to reach the nearest multiple of 45° (45°, 135°, 225°, 315°). Information technology can decide where to finish because when y = x, it has reached 45°. The reason for using these angles is shown in the higher up picture: As 10 increases, it does not skip nor repeat any 10 value until reaching 45°. Then during the while loop, x increments by one each iteration, and y decrements by one on occasion, never exceeding ane in ane iteration. This changes at 45° because that is the signal where the tangent is rise=run. Whereas ascension>run before and rise<run after.

The 2nd part of the problem, the determinant, is far trickier. This determines when to decrement y. It usually comes after cartoon the pixels in each iteration, considering information technology never goes below the radius on the first pixel. Because in a continuous role, the office for a sphere is the office for a circle with the radius dependent on z (or whatever the third variable is), it stands to reason that the algorithm for a discrete(voxel) sphere would also rely on this Midpoint circle algorithm. But when looking at a sphere, the integer radius of some adjacent circles is the aforementioned, but information technology is non expected to have the aforementioned exact circle side by side to itself in the same hemisphere. Instead, a circle of the same radius needs a dissimilar determinant, to allow the curve to come in slightly closer to the center or extend out further.

• One hundred fifty concentric circles drawn with the midpoint circle algorithm.

• 

  On left, all circles are drawn black.

• 

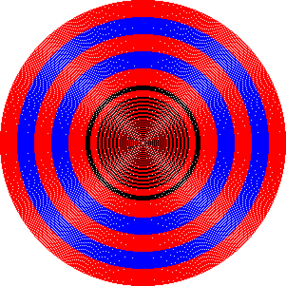
  On correct, cherry, black and blue are used together to demonstrate the concentricity of the circles.

Algorithm [edit]

The objective of the algorithm is to approximate the bend ${\displaystyle ten^{two}+y^{2}=r^{ii}}$ using pixels; in layman'southward terms every pixel should be approximately the same distance from the center. At each stride, the path is extended past choosing the adjacent pixel which satisfies ${\displaystyle x^{2}+y^{two}\leq r^{2}}$ simply maximizes ${\displaystyle ten^{2}+y^{2}}$ . Since the candidate pixels are next, the arithmetic to calculate the latter expression is simplified, requiring only bit shifts and additions. But a simplification tin can be washed in order to sympathise the bitshift. Continue in mind that a left bitshift of a binary number is the same as multiplying with 2. Ergo, a left bitshift of the radius only produces the bore which is defined equally radius times two.

This algorithm starts with the circle equation. For simplicity, assume the centre of the circle is at ${\displaystyle (0,0)}$ . Consider commencement the first octant only, and draw a curve which starts at point ${\displaystyle (r,0)}$ and gain counterclockwise, reaching the angle of 45.

The fast direction hither (the ground vector with the greater increment in value) is the ${\displaystyle y}$ direction. The algorithm always takes a pace in the positive ${\displaystyle y}$ direction (upwardly), and occasionally takes a step in the irksome management (the negative ${\displaystyle x}$ direction).

From the circle equation is obtained the transformed equation ${\displaystyle x^{ii}+y^{ii}-r^{2}=0}$ , where ${\displaystyle r^{2}}$ is computed simply once during initialization.

Allow the points on the circle be a sequence of coordinates of the vector to the indicate (in the usual basis). Points are numbered according to the social club in which drawn, with ${\displaystyle n=1}$ assigned to the kickoff point ${\displaystyle (r,0)}$ .

For each point, the post-obit holds:

${\displaystyle {\brainstorm{aligned}x_{n}^{2}+y_{n}^{2}=r^{2}\end{aligned}}}$

This can exist rearranged thus:

${\displaystyle {\begin{aligned}x_{n}^{2}=r^{ii}-y_{northward}^{ii}\end{aligned}}}$

And likewise for the next point:

${\displaystyle {\brainstorm{aligned}x_{n+1}^{two}=r^{two}-y_{northward+ane}^{2}\end{aligned}}}$

Since for the commencement octant the next indicate will ever be at least 1 pixel higher than the last (but also at most 1 pixel college to maintain continuity), it is true that:

${\displaystyle {\begin{aligned}y_{n+one}^{2}&=(y_{north}+i)^{2}\\&=y_{northward}^{2}+2y_{north}+one\terminate{aligned}}}$

${\displaystyle {\begin{aligned}x_{n+one}^{two}=r^{two}-y_{n}^{2}-2y_{n}-1\end{aligned}}}$

So, rework the next-point-equation into a recursive one by substituting ${\displaystyle x_{n}^{2}=r^{2}-y_{n}^{2}}$ :

${\displaystyle {\brainstorm{aligned}x_{n+1}^{ii}=x_{n}^{2}-2y_{due north}-one\end{aligned}}}$

Considering of the continuity of a circumvolve and considering the maxima along both axes is the same, clearly it will not be skipping ten points as it advances in the sequence. Usually it stays on the same x coordinate, and sometimes advances by one.

The resulting coordinate is and then translated by adding midpoint coordinates. These frequent integer additions practise not limit the operation much, as those foursquare (root) computations can exist spared in the inner loop in plough. Once again, the zero in the transformed circle equation is replaced by the fault term.

The initialization of the fault term is derived from an showtime of ½ pixel at the offset. Until the intersection with the perpendicular line, this leads to an accumulated value of ${\displaystyle r}$ in the error term, so that this value is used for initialization.

The frequent computations of squares in the circle equation, trigonometric expressions and square roots can again exist avoided by dissolving everything into single steps and using recursive computation of the quadratic terms from the preceding iterations.

Variant with integer-based arithmetic [edit]

Just as with Bresenham's line algorithm, this algorithm can be optimized for integer-based math. Because of symmetry, if an algorithm can be found that merely computes the pixels for one octant, the pixels can be reflected to get the whole circumvolve.

We start by defining the radius error as the divergence between the exact representation of the circumvolve and the center bespeak of each pixel (or whatsoever other arbitrary mathematical point on the pixel, so long as it's consistent beyond all pixels). For whatsoever pixel with a center at ${\displaystyle (x_{i},y_{i})}$ , the radius error is defined every bit:

${\displaystyle RE(x_{i},y_{i})=\left\vert x_{i}^{ii}+y_{i}^{2}-r^{ii}\right\vert }$

For clarity, this formula for a circle is derived at the origin, but the algorithm tin be modified for any location. It is useful to beginning with the bespeak ${\displaystyle (r,0)}$ on the positive 10-axis. Considering the radius will exist a whole number of pixels, clearly the radius mistake will be zero:

${\displaystyle RE(x_{i},y_{i})=\left\vert x_{i}^{2}+0^{ii}-r^{ii}\right\vert =0}$

Because it starts in the first counter-clockwise positive octant, it will step in the direction with the greatest travel, the Y direction, so it is clear that ${\displaystyle y_{i+1}=y_{i}+i}$ . Also, because information technology concerns this octant only, the Ten values have only 2 options: to stay the same as the prior iteration, or subtract past ane. A decision variable can be created that determines if the following is true:

${\displaystyle RE(x_{i}-1,y_{i}+1)<RE(x_{i},y_{i}+1)}$

If this inequality holds, then plot ${\displaystyle (x_{i}-i,y_{i}+1)}$ ; if not, then plot ${\displaystyle (x_{i},y_{i}+1)}$ . And then, how to make up one's mind if this inequality holds? First with a definition of radius error:

${\displaystyle {\begin{aligned}RE(x_{i}-ane,y_{i}+1)&<RE(x_{i},y_{i}+i)\\\left\vert (x_{i}-i)^{2}+(y_{i}+one)^{ii}-r^{ii}\right\vert &<\left\vert x_{i}^{2}+(y_{i}+ane)^{two}-r^{two}\right\vert \\\left\vert (x_{i}^{ii}-2x_{i}+1)+(y_{i}^{2}+2y_{i}+1)-r^{two}\right\vert &<\left\vert x_{i}^{2}+(y_{i}^{2}+2y_{i}+1)-r^{two}\right\vert \\\stop{aligned}}}$

The absolute value function does non aid, then foursquare both sides, since a square is ever positive:

${\displaystyle {\begin{aligned}\left[(x_{i}^{2}-2x_{i}+i)+(y_{i}^{2}+2y_{i}+1)-r^{two}\right]^{2}&<\left[x_{i}^{two}+(y_{i}^{2}+2y_{i}+1)-r^{2}\correct]^{ii}\\\left[(x_{i}^{2}+y_{i}^{2}-r^{2}+2y_{i}+i)+(1-2x_{i})\right]^{2}&<\left[x_{i}^{ii}+y_{i}^{2}-r^{2}+2y_{i}+1\right]^{2}\\\left(x_{i}^{2}+y_{i}^{ii}-r^{2}+2y_{i}+one\right)^{ii}+2(1-2x_{i})(x_{i}^{2}+y_{i}^{2}-r^{two}+2y_{i}+one)+(i-2x_{i})^{2}&<\left[x_{i}^{2}+y_{i}^{2}-r^{2}+2y_{i}+ane\right]^{2}\\2(one-2x_{i})(x_{i}^{2}+y_{i}^{2}-r^{2}+2y_{i}+1)+(ane-2x_{i})^{ii}&<0\\\stop{aligned}}}$

Since x > 0, the term ${\displaystyle (i-2x_{i})<0}$ , and so dividing gets:

${\displaystyle {\begin{aligned}2\left[(x_{i}^{2}+y_{i}^{two}-r^{two})+(2y_{i}+1)\right]+(ane-2x_{i})&>0\\2\left[RE(x_{i},y_{i})+Y_{\text{Modify}}\right]+X_{\text{Change}}&>0\\\end{aligned}}}$

Thus, the conclusion criterion changes from using floating-point operations to simple integer addition, subtraction, and bit shifting (for the multiply by 2 operations). If ${\displaystyle 2(RE+Y_{\text{Change}})+X_{\text{Modify}}>0}$ , then decrement the X value. If ${\displaystyle 2(RE+Y_{\text{Modify}})+X_{\text{Modify}}\leq 0}$ , then keep the same Ten value. Again, by reflecting these points in all the octants, a full circle results.

We may reduce computation past only calculating the delta between the values of this decision formula from its value at the previous stride. We outset by assigning ${\displaystyle E}$ every bit ${\displaystyle 3-2r}$ which is the initial value of the formula at ${\displaystyle (x_{0},y_{0})=(r,0)}$ , then as higher up at each step if ${\displaystyle E>0}$ we update it as ${\displaystyle Due east=E+2(5-2x+2y)}$ (and decrement X), otherwise ${\displaystyle Due east=E+2(3+2y)}$ thence increment Y as usual.

Drawing incomplete octants [edit]

The implementations above always describe only complete octants or circles. To draw only a certain arc from an angle ${\displaystyle \blastoff }$ to an angle ${\displaystyle \beta }$ , the algorithm needs first to calculate the ${\displaystyle 10}$ and ${\displaystyle y}$ coordinates of these end points, where it is necessary to resort to trigonometric or square root computations (see Methods of calculating square roots). Then the Bresenham algorithm is run over the complete octant or circle and sets the pixels only if they fall into the wanted interval. After finishing this arc, the algorithm tin exist ended prematurely.

If the angles are given as slopes, then no trigonometry or square roots are necessary: just check that ${\displaystyle y/x}$ is betwixt the desired slopes.

Generalizations [edit]

It is also possible to use the same concept to rasterize a parabola, ellipse, or any other 2-dimensional bend.^[four]

References [edit]

1. ^ Donald Hearn; M. Pauline Baker (1994). Computer graphics . Prentice-Hall. ISBN978-0-13-161530-four.
2. ^ Pitteway, One thousand.50.V., "Algorithm for Cartoon Ellipses or Hyperbolae with a Digital Plotter", Computer J., x(3) November 1967, pp 282-289
3. ^ Van Aken, J.R., "An Efficient Ellipse Drawing Algorithm", CG&A, four(9), September 1984, pp 24-35
4. ^ Zingl, Alois (December 2014). "The Beauty of Bresenham'southward Algorithm: A simple implementation to plot lines, circles, ellipses and Bézier curves". piece of cake.Filter. Alois Zingl. Retrieved xvi February 2017.

External links [edit]

• Drawing circles - An commodity on cartoon circles, that derives from a simple scheme to an efficient one
• Midpoint Circumvolve Algorithm in several programming languages

persaudcrist1978.blogspot.com

Source: https://en.wikipedia.org/wiki/Midpoint_circle_algorithm

Share this post